Physics relies heavily on quantifying the natural world. But each time you measure a physical quantity, a small amount of uncertainty creeps in. And one of the key reasons? The least count of your instrument, that is, the smallest value your tool can measure with true precision.
No matter how advanced your instrument is, every measurement has limits. That’s where significant figures come in. They show how many digits in a measurement are meaningful, based on the instrument’s resolution.
Whether you’re finding the speed of a car or the energy of a moving object. Significant figures help ensure that you only report what our tools can reasonably measure.
In this article, you’ll learn what significant figures are, the rules for determining them, and how to apply arithmetic operations on them.
What are Significant Figures in Simple Words?
In any measured value, we count all the digits we know for sure, plus the first digit we guess, as significant figures.
These digits are also known as significant digits, or informally just sig figs.
Let’s understand this definition with an example. Suppose you draw a line on a paper and want to measure its length with a meter rule having a least count of 0.1 cm.
The end of the line falls between 13.7 cm and 13.8 cm.
Here we follow a simple rule: if it’s before the halfway point, write the previous division, i.e., 13.7 cm. If it reaches or goes past the halfway point, write the next division, i.e, 13.8 cm.
By following the above rule, the length of the line is recorded as 13.8 cm. In this example, you know 1 and 3 for sure, but for the digit 8, you guessed because of the limitation of the instrument.
According to the definition, the value has 3 significant figures.
If you have a more advanced instrument that can measure to hundredths of a centimeter. You will have the more precise value up to 4 significant figures, e.g., 13.78 cm.
Here, 1, 3, and 7 are known exactly, while 8 is the first uncertain digit. So, you now have 4 sig figs.
As our instruments become more advanced, we can measure value more precisely and accurately.
Rules to Determine How Many Significant Figures Are in a Measurement
1. All digits from 1 to 9 in a measurement are always significant.
There are special rules for zeros that determine whether they count as significant figures or not, as outlined below:
2. A zero between two significant digits is also significant. For example, 19,101. It has 5 significant digits.
3. Leading zeros: Any zeros that appear before the first non-zero digit do not count as significant.
They just act as placeholders to show the decimal position. For example, 0.005 has only 1 significant digit (i.e., 5).
If you measure this value with an instrument that has a least count of 0.001, you count like this: 0.002, 0.003, 0.004, 0.005. As you can see, only the non-zero digit (5) is actually being measured, while the zeros on the left are just placeholders.
4. Trailing zeros: Zeros that come after the last non-zero digit may or may not be significant.
If there is a decimal point present in the number, then the trailing zeros are significant. For example, 50.0 has 3 significant figures.
If a number has no decimal point, the instrument’s least count tells you how many trailing zeros are significant.
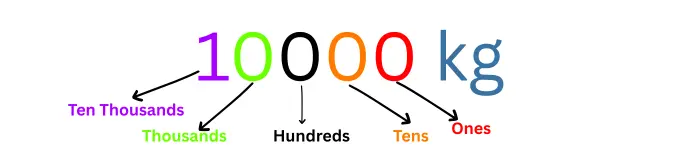
For example, you have an object that has a mass of 10,000 kg, and the measuring instrument with a least count of 1 kg.
This means the instrument can measure all the digits accurately, except the last one, which you have to estimate because of the instrument’s limit.
In this case, the number of significant figures, according to the definition, is 5.
However, if the instrument has a least count of 10 kg, it can measure all digits accurately except the tens place, which can only be estimated. The ones place cannot be measured at all.
In other words, the instrument can measure values like 10,000 kg, 10,010 kg, 10,020 kg, and so on, but it cannot detect 10,001 kg, 10,002 kg, etc.
Here, the number of significant figures is 4.
So, when you record measurements, always mention the instrument’s least count or place the decimal point correctly.
If there are trailing zeros but you don’t know the instrument’s least count or there’s no decimal point, don’t count those zeros as significant figures. For example, 899000 has 3 sig figs.
5. It is better to express the results in scientific notation to avoid any ambiguities. In scientific notation, all the digits in the number before the ×10 part are significant.
For example, 10,000 kg can be written as 1.00 × 10⁴ kg in scientific notation, if the least count is 100 kg. The number 1.00 before the ×10 has three digits, so all three are significant figures.
Include trailing zeros in the coefficient only if they are meaningful, based on the instrument’s least count. These zeros indicate the precision of the measurement and reflect the significant figures.
Significant Figures Examples for Better Understanding
The table below gives examples to help you understand how to determine significant figures in a measurement.
| Measured Value (Unit) | Significant Figures | Explanation |
|---|---|---|
| 0.07 | 1 | There is only one non-zero sig fig. Leading zeros are not significant. |
| 34.0 | 3 | There are 2 non-zero sig figs and one trailing zero sig fig. |
| 100 | 1 | There is one non-zero significant digit. Trailing zeros are not significant if there is no decimal point or information of least count. |
| 10.00 | 4 | There is one non-zero significant figure and three trailing zeros sig figs. |
| 1.3450 x 103 | 5 | There are 4 non-zero significant digits and one trailing zero in the number before x10 that is also significant. |
| 20.40 | 4 | There are 2 non-zero sig figs, one zero is between two non-zero digits, and one trailing zero, which is significant as there is a decimal point. |
| 0.00340 | 3 | There are 2 non-zero significant digits and one trailing zero sig fig. Leading zeros are not significant. |
Note: Converting the units shouldn’t change the number of significant figures. For example, if you convert the 0.453 mm to 4.53 cm, the significant figures would be the same, which are 3.
Unit conversions often cause confusion, for example, when turning 540 mm into 0.540 m.
Some people think 540 mm has 2 significant figures, and converting to meters makes it 3 sig figs. This is not correct.
The number of significant digits is determined by the precision of the measurement, which comes from the instrument’s least count.
Changing the unit doesn’t increase or decrease the significant digits.
- If the instrument’s least count is 1 mm, then 540 mm has 3 significant figures. When converted to meters, it becomes 0.540 m, still with 3 significant figures.
- If the instrument’s least count is 10 mm, then 540 mm has only 2 significant figures. In meters, it should be written as 0.54 m, reflecting 2 significant figures.
When converting units, make sure the digits show the measurement’s precision and only include trailing zeros that matter.
There is one more problem that needs explanation. How many significant figures are in 0.0 cm? As there’s no non-zero digit, the usual rules for leading and trailing zeros don’t directly apply.
In this case, the answer is in the precision of the measuring instrument.
Suppose your instrument measures to the tenth place (i.e., least count 0.1 cm), and the actual value lies between 0.0 and 0.1 cm.
Even if the real value is something like 0.03 cm, the instrument cannot detect it and rounds it to 0.0 cm.
According to the rules, all reliably known digits plus the first estimated digit are considered significant. Here:
- The zero before the decimal is just a placeholder → not significant
- The zero after the decimal is the first estimated digit from the instrument → significant
So, 0.0 cm has 1 significant figure, reflecting the precision of the measurement.
It rarely happens because for such a small quantity, we usually go with instruments having the least count with more precision.
That’s why no specific rule exists for these types of values.
Significant Figures in an Exact Number
Exact numbers are known with complete certainty, so they are treated as having infinitely many significant figures. Because they have no uncertainty, they never limit the precision of any calculation. For example,
Counting numbers like 7 apples or 12 students is exact. These values are exact, so they count as having unlimited significant figures.
Defined values, such as 1 second or 1 meter, are exact because the definition fixes their value, giving them infinitely many significant digits.
Some physical constants, like the speed of light (299,792,458 m/s), have infinite significant figures because their values are exact.
Significant Figures Rules for Arithmetic Calculations
These rules rely on the idea that a result can’t be more precise than its least precise measurement.
1. Calculating Correct Number of Sig Figs When Multiplying and Dividing
When you multiply or divide measurements, the final answer should have the same number of significant digits as that of the measured value with the least number of significant digits.
While multiplying/dividing, the absolute uncertainties grow proportionally to the magnitude of the result.
So, the relative (or fractional) uncertainties of the numbers add up, not the absolute ones.
The number with the fewest sig figs usually has the largest relative uncertainty, which limits the precision of the result.
Let’s understand this rule with an example. Suppose you measure a rectangle:
- Length = 4.2 m (2 sig figs)
- Width = 3.56 m (3 sig figs)
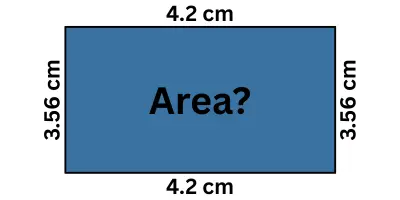
And want to calculate its area:
\(Area=Length\times Width\)
\(4.2\times3.56=14.952\;\mathrm{cm}^2\)
The calculator gives 14.952 cm², but this is more precise than the measurements allow. Using the rule, the final answer should match the number with the fewest significant figures, which is 2 here.
So, you have to write the answer with 2 significant figures. The extra digits beyond that are meaningless and give a false sense of accuracy.
Delete these extra digits.
When deleting digits, round off the last significant digit that will be retained.
There are certain rules for rounding significant figures that must be taken into account when rounding. Those are mentioned below
- If the 1st non-significant digit after the last significant digit is less than 5, you leave the last significant digit as it is.
- If that digit is greater than 5, you increase the value of the last significant figure by 1.
- If the digit is exactly 5, then
- If the last significant digit is odd (1, 3, 5, 7,…), increase it by 1.
- If it is even (0, 2, 4, 6,…), leave it unchanged.
Following these rules, the final answer of the above multiplication is 15 cm2, which in scientific notation becomes 1.5 x 10 cm2.
Rounding Significant Figures Examples for Better Understanding
| Number | Round to | Final Number |
|---|---|---|
| 43.75 | 3 sig figs | 43.8 |
| 56.8546 | 2 sig figs | 57 |
| 7324454 | 4 sig figs | 7324000 |
| 1000 | 3 sig figs | 1.00 x 103 |
| 0.04203425 | 5 sig figs | 0.042034 |
Similarly, if you divide two numbers: 23.567 kg and 34 cm3.
\(\frac{23.567}{34}\) kg cm-3
The final answer that we get with the help of a calculator is 0.693147058824.
Because 34 is the value with the lowest number of significant figures, the final result should be expressed using two significant figures: 0.69 kg cm-3 or 6.9 × 10-1 kg cm-3.
2. Calculating Correct Number of Sig Figs When Adding and Subtracting
When you add or subtract measured numbers, round the final answer to the position of the first doubtful digit of the least precise value.
While adding or subtracting, the units of all the measurements should be the same.
Example:
Addition: 23.454 g, 224.1 g, and 23.34 g
As the least precise measured value has a doubtful digit at the tenth place.
So, the correct result, after rounding off, is 270.8 g.
Let’s take one more example to make the concept clearer. Here we take two lengths in meters, having values
- 235000
- 34352
235000 + 34352 = 269352
Since, the least precise number, 235000, has the first doubtful digit at the hundreds place. In the answer, all the digits after that do not give reliable information (i.e., they are not significant). So, the correct answer is 269000.
How to do Sig Figs with Mix Operations?
When a calculation has more than one operation, follow the rules at each step, but round off only in the final answer.
The reason behind it is that every time you round an intermediate result, you lose information.
That small loss gets carried into the next calculation step and can compound, producing a final answer that’s less accurate than it should be.
For example: (120.0 – 87.55) ÷ 4.88
According to the BODMAS rule, the operation in the bracket should be carried out first. After subtraction, you get,
32.45 ÷ 4.88
Applying the addition/subtraction rule, the first number now has 3 sig figs (3, 2, 4). Don’t round yet, underline the last sig fig, and write it like this:
32.45/4.88
When performing this operation via calculator, the result you get is 6.64959016393.
Here, apply the rule of division/multiplication. Then round off the final answer as well. The result after applying the rule and rounding off is 6.65.
